As I was gathering resources and reference for Calculus. I ran by a page (that I cannot locate now), of a math tutor that made a small comment about how he also had a Rubik's cube solving page.
Flash back at least 11 years ago.
For a holiday (I can't remember which) my girlfriend of at least 8 years years (who is now my wife of 10 years) gave me a picture cube as a gift.
After briefly looking at all the pictures of our life together, in fast, deliberate motions, I scrambled the cube. The look of horror on my future's wife face is still etched in my mind.
I looked down at the cube and shared her concern. I had never solved a Rubik's Cube. We knew no one who had, therefore this cube of our pictures would never be rearranged again.
I gave it all I had, for hours and days and weeks I tried to solve it. But I could not. The cube sat in my car for at least two years. One day, after we got married, my wife found it and gave it a sad forlorn look. She took it and stored it with the rest of our pictures and heirlooms. I felt like the worst person on earth for being foolish enough to scramble that picture cube.
Flash forward to two weeks ago.
When I saw that page on how to solve a Rubik's Cube using algorithms. I knew what I had to do.
As fate had it, one day we were shopping at Party City and they were selling mini Rubik's cube for 89 cents. I grabbed one as casually as I could and bought it.
Like I said, I never found the first page I used, but afterwards I got these others and these were the ones that helped me the most. Beginner's Solution to the Rubik's Cube. Beginner's Rubik's Cube Solutions. In the beginning, as I read these I felt overwhelmed, almost as overwhelmed as I felt doing Calculus without precalculus back in January. They were talking about Faces, primes, clockwise and counter-clockwise moves. They also mentiones middle pieces, corner pieces, edge pieces. Then they would give me string of algorithms that looked like this: R2 U F B' R2 F' B U R2.
There was no way this could work, could it? My first attempt with my mini cube, after at least 3 hours, ended in utter failure. My wife, who thought I had gotten my self another hobby besides calculus was not impressed. I had kept my real intentions secret from her. And on top of everything, she thought I was just cheating using formulas to solve a cube. At the time, so did I. I felt like I was painting by numbers. All I had to do was follow those instructions to the letter and I would solve a cube.
By the time I had solved my mini cube, I felt otherwise. This was not painting by numbers. Solving a Rubik's cube with the beginner method was about recognizing patterns and executing moves to make the pieces go where you wanted them to...without messing with the other pieces you had already done.
After solving my mini cube, I did not feel ready enough to tackle our picture cube. So I looked for more practice. I got the Rubik's cube app for my iPhone and Ipad and bought a "magic cube" from China on EBay. My goal was to practice with these as much as I could.
As I waited for my Chinese cube to arrive, I practiced with the app. I found it hard to use at first because the controls were weird. But after a while, I was "fluent" in it.
Still remembering the combination of moves that I needed to make and when I was supposed to make them still took me a long time.
My first time solving a cube in the app took me 1 hour 49 minutes. And I had to refer back and forward to my notes. More than once my wife found scraps of paper with algorithms on them...I got some weird looks from her.
The great thing about having the app is that I could fire it up at a moments notice if I was waiting in line, in an elevator, or in my lunch break. I could even pause the game and pick it up later at night right before bed. I was getting good practice out of this. After 5 tries I could keep my time under an hour. After 10 tries I could solve it a shade under 15 minutes. In the last 5 tries I could solve a cube in about 6 minutes.
I now felt ready to solve our picture cube.
All last week I have been asking my wife if she remembered were we had put that picture cube. I still did not tell her what I wanted to do, but I knew she knew. What I bet she did not know was that I could solve it this time. After a few attempts at finding it, and making a mess of our closet, I got my hands on it. The cube felt weirdly solid in my hand. As if it had gathered the mass of 10+ years just waiting for this moment.
I looked at it and remembered how hard I had tried to solve it the last time. Yet, all that was solved was a single face. It showed a picture of a kiss I gave my future wife after I had caught the garter from my brother-in-laws wedding. I would propose to María soon after that. It seemed fitting that I would attempt solve this cube on the year of our 10th wedding anniversary.
However, after I look a the rest of the pictures, I panicked. I could not tell which pieces belonged together. Many of the pictures had parts that were almost the same color. This would not be as easy as I had hoped. María was walking around the house doing some stuff and would check in me from time to time. When she did I asked her questions that must not have been reassuring to her like: where do you think this piece goes? She would give me her best guess and walk on.
After about 20 minutes it all clicked and I was back on track. A minute later I had solved all the pieces. However, I was not done. This is a picture cube which has a key difference than a regular cube.
In a picture cube the center pieces need to be rotated to fit the rest of the pattern. If you don't, you will have a solved cube looking like my mini cube did: I bet Jessie would love to have her face back in its proper orientation. Before you say anything...yes, my mini cube was of Toy Story...moving on!
Having centers not rotated properly can be quite distressing to many people. Because you can actually see it happening while you are solving the cube. If you type, Rotate center pieces, in google, you will get dozens of hits on this problem and how to solve it. The one I found to help me most was this video. The process involved a very simple algorithm repeated 5 times to turn a center piece 90 degrees clockwise and another center piece counterclockwise.
To finish my cube I would have to do the algorithm twice. Since I had to do 4 moves to complete the instructions once. That meant I had to do 40 moves to rotate all center pieces to their proper place. If I make a single mistake, I could scramble the cube in such a way that all my effort would be wasted. And guess what, at move 38, I lost track of my next move. I had no idea what I had to do next and the cube looked horribly scrambled.
I was heartbroken. I knew I was really close, but if I made the wrong move It was over. I just sat there, looking at all the faces of the cube and see if I could get back on track. A week ago I would have been lost, but after all that practice, I could see the relationships between pieces clearer. I felt a rush of adrenaline as my brain registered that I had already solved the cube. It must be the same rush a chess player gets when he or she knows the game has already been won a few moves ahead. I took a deep breath and mave the last two turns.
And there it was...solved. After all those years.
I showed it to María and the look on her face was amazing. I sat her down and told her how this cube had been on my mind for many years. how I always wanted to solve it. To rearrange all those pictures of our lives together. It was symbolic for me. And then she told me something that melted my heart.
A Rubik's cube has 54 squares. 9 squares per face per 6 faces. María told me that When our picture cube arrived the first time her hands. She was disappointed. The sticker that had the pictures looked really fragile to her. She knew that unless she did something, it would deteriorate and fade really soon. So she cut 54 squares of clear adhesive paper and covered all of them, one by one. It must have taken her hours of painstaking and risky work to get that cube to me. No wonder she was so chocked when I just scambled it the first time, and so sad when she found it still unsolved.
Now that we had it back we put it in a place of honor. Our bedroom table. To be looked upon by us and our little girl for many years to come.
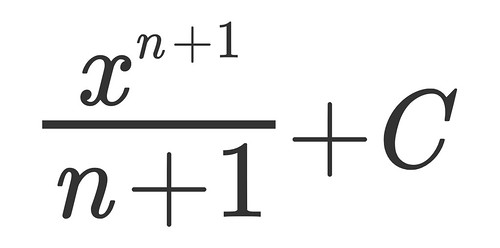
 But until I know what that constant actually is, I will not know the original formula.
But until I know what that constant actually is, I will not know the original formula.