As I near the end marker of this journey of learning calculus I meet anti-derivatives. And I am glad I did. Somehow this concept helped me put into perspective all the concepts that have come before it and makes me feel I am back on track again. Just in case you were wondering where I lost my way, it was somewhere into L'hopital's Rule.
First things first: What is an Anti-derivative?
Well an anti-derivative answers the question of: what is this formula a derivative of? Or from what original formula could we have gotten this derivative. For example, if we have x2 (the squaring function), it's derivative is 2x. Therefore, x2 is an anti-derivative of 2x. (For formal definition go here)
Notice that I wrote that x2 is an anti-derivative of 2x. This is important because there can be many anti-derivatives for a given function. If we consider this formula for an anti-derivative: xn+1/n+1+C, (which looks a lot prettier in pictures, see bellow) there is a constant C that is introduced. The way I understand it is that there is only so much information a anti-derivative can give you. In order to recover a specific formula from it's derivative you need to know where that functions "started".
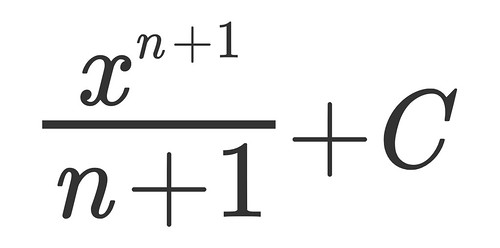
To complete the argument above, let now imagine this scenario. I know that -2x+5 is a derivative of a function I am interested in knowing. Using the ati-derivative formula I get that the function I am interested in is:
But what is C? I have no clue with the information I was given. Let's say I know C is a whole number between 1 and 4. A graph can show me what to expect the graph to be.
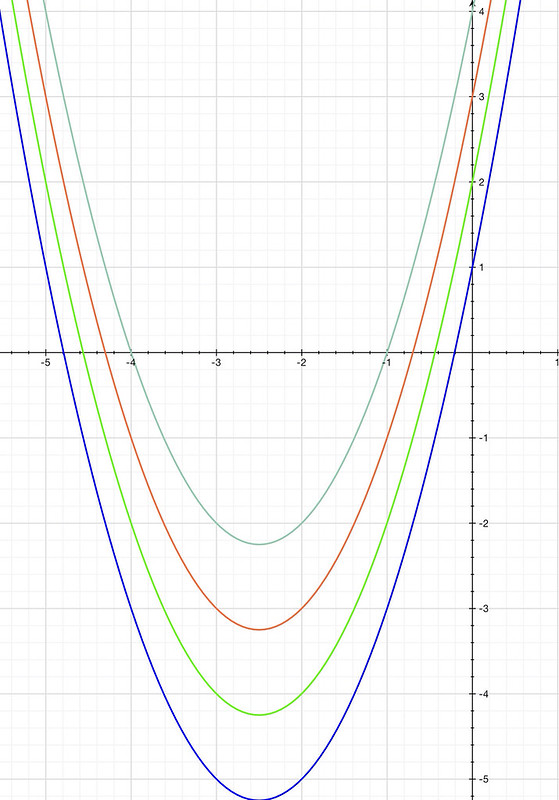 But until I know what that constant actually is, I will not know the original formula.
But until I know what that constant actually is, I will not know the original formula.
In the picture opposite I have 4 possible graphs, each passing through the y (vertical axis) at 1,2,3 and 4. All 4 graphs are exact copies of the formula I am looking for, but they "start" at different points C.
For a great explanation about how C is relates to anti-differntiation in terms of position and velocity. Check out this video from my Mooculus course. I liked this video not only because Dr. Fowler seemed to have had had too much coffee, but because his explanation incorporates the steps to solve an anti-differentiation equation that has "physical" applications.
Anti-differentiation is an important bridge in my road to understand calculus. At least that is the promise that was made by my professor when he introduced the topic. Whether that is the case or not, I find it fascinating that having information about a function, I can derive other functions that are related, and give me additional information about the original one.
Let me know what you think in the comments.