The derivative of a function gives us important information about the function being examined. That is a very cool idea. It is basically metadata about how the original function will behave. The derivative of a function, using a very basic explanation which is what I can manage with my knowledge, describes whether a function is increasing, decreasing, and/or changing direction, in other words, it gives you the rate of change.
The derivative also gives us the slope of the tangent line for any point along a function that is differentiable. In other words, if we know the derivative and a point along the function, we can calculate the tangent line for that point.
It bet there a lot of other things the derivative tells us, but these two are the ones that fascinated me the most.
The more I think about it the more it sinks in that calculus is about change. Or in the words of professor Jim Fowler from Mooculus, about how "wiggling the inputs affect the outputs".
Let's do an example: Imagine we have a toy rocket which we shoot up into the sky and watch it fall to the ground. A formula that describes the trajectory of the rocket is: y=-x^2+4x where x=time in seconds and y is feet. In one second it's 3 feet high, in 2 seconds it's 4 feet high. It's average climb from zero to 1second is 3 feet per second and from 1 to 2 seconds it's 1 feet per second. But what how fast was the rocket climbing at exactly 1 second?
The derivative can help us with that. Using the derivative rules:
The derivative of -x^2+4x is -2x+4. And once we know the derivative, and understand that the derivative is the slope of the tangent line at a given point, and remember that the derivative at a point gives us the instantaneous rate of change of a function, we can do some algebra to know how fast the rocket was climbing at exactly 1 second:
-2(1)+4= instantaneous speed
-2+4= 2 feet per second
So at 1 second the rocket is climbing 2 feet per second.
What happens at 2 seconds?
-2(2)+4=0
At 2 seconds the rocket is moving at 0 feet per second, therefore it's standing still.
And at 3 seconds?
-2(3)+4=-2
Interesting, at 3 seconds the rocket is not climbing but declining at 2 feet per second.
We know the rocket hits the ground at 4 seconds. How fast was it going?
-2(4)+4=-8
The rocket hit the ground declining at 8 feet per second.
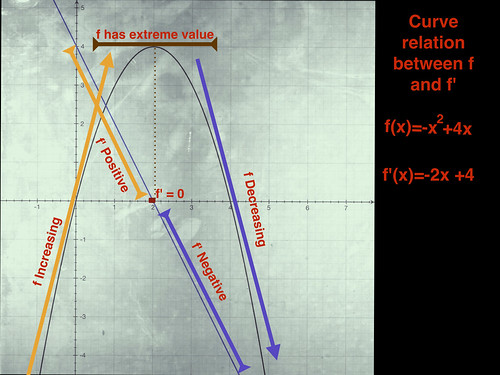
When we look at the graph we can see these numbers make sense. The parabola starts steeply (the rocket is climbing fast but slowing down), then levels off to a point where there is no more climb (the rocket stands still), and then the parabola declines steeply, (the rocket falls accelerating until it reaches the ground). That was really cool. Now if we look at the graph formula of the derivative by itself, it would have told some key elements of the original function.
-2x+4 is a line. And this line is positive from time 0 to 2 seconds, at 2 seconds it crosses the y axis and is negative until 4 seconds. Looking at that graph and using the first derivative test, we can conclude that from time 0 to 2 seconds the original graph -x^2+4x is increasing in the interval, that at 2 seconds there is a local extreme value where the graph changes direction, and we can also see that from 2 to 4 second the graph is decreasing in the interval. What this means is the if I had the function of the derivative but not the original function I could make some intelligent guesses as to how the original function would behave. Now that to me is amazing.
Like I mentioned before, I have been taking a calculus course for about two months now. Therefore the basics of the derivative is something that has long passed. If fact, it took me a couple of hours to find an explanation of it that I could use in order to post it. This problem got me thinking about the depth of my learning. I know I already covered some of these insights in earlier posts about learning for testing and grades, versus learning to understand.
You see, I was feeling quite confident going week to week in my calculus course, at least at the beginning. That was because I was doing the minimum study required to pass the quizzes. And then, when the concepts started to stack up, I found myself lost. I fear this is what is wrong with the way we educate in Puerto Rico and the United States. If we are teaching to tests, then the students will study to pass those tests and might not explore what the knowledge in itself means. That might mean that the best product we could be creating is excellent test takers instead of excellent thinkers.


No comments:
Post a Comment