Here I am. At the end of my project. My next to last post. And my topic is the fundamental theorem of Calculus. Like the name says, this theorem is a pretty big deal. Let's start by what the Theorem says according to Wolfram Alpha:
I can proudly say I actually understood some of that, but at first could not yet grasp the implications that statement had on all I had studied so far.
Here is Dr. Fowler from Mooculus.com explaining this theorem and it's implications brilliantly:
Now here is what (I think) the fundamental theorem of calculus means in my own words. If you want to integrate acontinuous function on a closed interval, instead of doing the limits of the Riemman Sum applicable, just find the anti-derivative of the function you need to integrate and substract the result of the evaluation of that anti-derivative at the befining and end points of your closed interval.
Or in better words, forget about integrating, just anti-diferentiate!
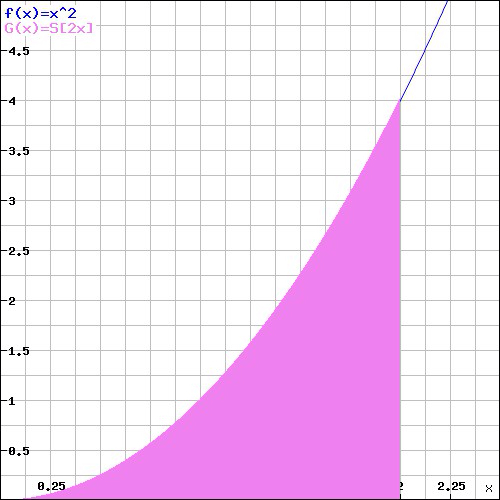
In my last two posts I had been searching for the area under the curve of x2 from the interval 0 to 2. And I had to do a bunch of sigma calculations and set up Riemman Sums and then even take a limit in order to get to 2.667 square units which is 8/3.
The fundamental theorem of calculus is, as I see it, a reward for all my efforts. It is a way of saying:"Fernando, you have toiled and fret, and sweated over these sums and spend countless pages calculating and recalculating all these stuff. You have earned a shortcut." Why thank you very much calculus!
Do you want to check out my new super power? Ok.
The FTOC is telling me that to integrate from the interval a=0 to b=2 of the function x2 all I need is an anti-derivative of that formula which I will proceed to evaluate at both points of my interval and then subtract. What is an antiderivative of x2?
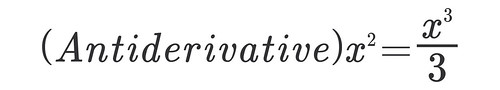 Technically there is a + C after that formula but I am assuming it is 0, check Dr. Fowler's video again for that to make sense.
Technically there is a + C after that formula but I am assuming it is 0, check Dr. Fowler's video again for that to make sense.Ok, so now I have my antiderivative x3/3 and I am ready to evaluate it at 2 (b=2) and at 0 (a=0) and then take the difference .
There you have it, the elusive 2.667, the area under the curve of x2 From the interval starting at 0 ending at 2.
Wow, that took way less effort than before. However, If I had not passed through all those previous steps, all that trouble and effort, I would not have appreciated the beauty, simplicity and deeper meaning of what I have accomplished.
This is my next to last post in this blog and it is a fitting one. I cannot begin to express the emotions I feel at the moment. I have attained great insights in this journey. I now have a deeper understanding of math and the world around me.
Let me know your thoughts in the comments section.

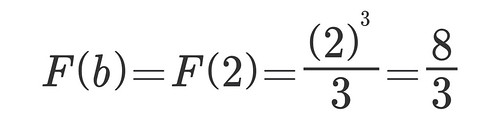



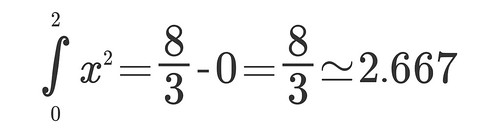
Thank you for writing this. I am very glad to see how much you've accomplished!
ReplyDeleteHighly informative details been imparted by you. I like the way you share useful data in a representative way, making it easy for many readers to understand. Best tuition services are provided by TheTuitionTeacher in Delhi.
ReplyDeleteHome Tutors in Delhi | Home Tutors Delhi
Calculus is a strong mathematical instrument that aids in the explanation of the world around us; it is more than just a chapter in mathematics. It has countless uses in fields ranging from engineering to economics and science. In addition to improving your CBSE Class 12 Mathematics, mastering calculus ideas and situations lays a strong basis for future education.
ReplyDeleteOnly on Edusession live can you learn more quickly, explore more, and understand every idea with ease.