Coursera Pre-Calculus Started

I mentioned a week ago that I had enrolled in a Coursera massive online course for Pre-Calculus from the University of California Irvine. The course will be 10 weeks long and I am halfway my first week.

 

I'll give my first impression of it: the course is great, and daunting, and frustrating at once. It comprises of short video lessons which are very well done even when some students complain that the voice of the instructor sounds like a "California Valley Girl". Hey, as long as she does not sound like Siri, I have no problem.

 

After the video there is a quiz of anywhere from 1 to 4 questions (at least for the ones I have completed). These quizzes test your superficial knowledge of the subject in the video. In other words they make you re-enact the video versus challenging you to apply the knowledge to a problem that is different. This makes sense since we are starting a review of concepts we will need for pre-calculus. If the patter continues later on it will be a disappointment.

 

The quizzes do present an unforeseen challenge, you have to use especial notation to get your answers input in. Anyone accustomed to using excel will find this simple, but for others it might be an extra worry. For example, if my answer is (5√2) ^-5 , I would have to write it like this: (5*sqrt(2))^-5. I know from excel that * means multiplication and that ^ goes before an exponent, but sqrt(number) would have thrown me for a loop. Fortunately bellow the answer box there is a button to verify your answers notation.

 

Another challenge from the quizzes (which the administrators have told us they are working on expediently), is that they some are flawed and do not accept a correct answer as correct. This can be a grief if you are not sure whether it is your answer or the quiz that is incorrect.

 

I have learned (well, re-learned would be more appropriate) a lot in half a week. Yet my best insights have come not from the course material but from my experiences. I list those insights bellow.

 

I have learned that:

• Using pencil and paper to work is better that doing it in your head.
• Rushed work will create shoddy answers.
• Knowing the math is not enough, it's the arithmetic that will get you.
• It is more exciting to get an answer wrong on your first attempt, since it leads to discovery.

I want to expand a little on that last sentiment. In the summer of 2012, scientists at the Large Hadron Collider at CERN, where fairly certain they had found the Higgs Boson, known as the God Particle, a theoretical particle that would explain how matter got mass. As the experiments were underway, I remember reading about renowned physicist who hoped the Higgs Boson was not be found. They were saying that finding it would close a big avenue of new physics. The act of being right would stymie discovery. At the time, I could not understand them. Now I do. Please do not think that I am comparing learning calculus to finding the God Particle. I just find that to get an exercise wrong forces me to look at the process, and the steps I followed. It makes me focus and see beyond what I think the answer should be. That is exciting. If I get the answer right the first time I feel like: "Well, that's that."

 

Sure enough, I am becoming a firm believer that mistakes make you better. What do you think about that?

 

All Students Take Calculus in SohCahToa

Mnemonics saved my skin more than a few times in school, be it Please Excuse My Dear Aunt Sally which is used to remember the order to solve operations (parenthesis, exponent, multiplication, division, addition, subtraction), or My Very Energetic Mother Just Served Us Nine Pizzas to remember the order of the planets from the sun. The last one worked very well until Pluto was demoted...now Mom Just Serves Us Nachos. Talk about a downgrade.

In life after school, Mnemonics are now often used to create secure passwords. I read about two ways to create stronger passwords with this technique: one is before the fact and the other after the fact. Before the fact means that you take a memorable phrase (either universally memorable or better yet personally memorable) and create a password using the first letter of each word in the phrase. For example: Hickory dickory dock,the mouse ran up the clock,the clock struck one,the mouse ran down,hickory dickory dock becomes hddtmrutctcsotmrdhdd. You could even substitute "one" for 1.

To create a mnemonic device after the fact means that once you get a secure password, you then create a phrase or technique to remember it. Here I used the Norton Secure Password Generator to create this one: NadEbr2v. My mnemonic for it would be Nadia and dear Ernest bought roses too violet.

In trigonometry I ran across two mnemonic devices, one is SohCahToa, which helps you remember the angles Sine, Cosine and Tangent relate to. Sine is Opposite over Hypotenuse; Cosine is Adjacent over Hypotenuse; Tangent is Opposite over Adjacent.

 

The other one is All Students Take Calculus, and it is used to remember which trig formulas have positive signs in the unitary circle, the concept of which I'll try to summarize out of my review.

 

As I understand it an unitary circle is one that has a radius of 1 and its center is in the (0,0) coordinate of a Cartesian plane. In trigonometry, this unitary circle is used to study the functions of sine, cosine, tangent and their counterparts. Since the unitary circles has a radius of 1, if we use that radius to create a right triange with the x axis, that trianangle and any other right triangle we create with a point on the unitary circle circumnsference, will have a hypotenuse of 1.

Therefore, as per the Pythagoras theorem, a^2 + b^2 would equal 1. Using SohCahToa we know that sine and cosine are the lenght of the opposite side and adjacent side of a triangle respectively, divided by the lenght of the hypotenuse. Since the hypotenuse is always 1 in the unitary circle the sine and cosine of any angle made in the unitary circle equal the lenght of the "legs" of that triangle. I think I did a better job explaining it in the picture here.

 

The Unitary Circle can also be used, I learned, to get the important points of a sine, cosine and tangent graph. What I mean by important points, are the points that distinguish those functions and that help people analyze them.

 

For example, imagine an unitary circle as a clock and substitute 12 o'clock for π/2, 9 o'clock for π, 6 ο'clock for 3/2 π and 3 0'clock is 0. Here we will make a mental image of a right triangle in that circle. If that triange has no height, does it have and opposite side? No, but there is point in the unitary circle there that is (1,0). Therefore at 0, sine is 0 but cosine is 1, which means the sine graph will start at 0 and the cosine graph at 1. If we take the point π/2 (12 o'clock), we can say that triangle has no base but there is a point (0,1) there. At that point the cosine graph is 0, but sine is 1. Following the same rules sine is 0 at π and cosine is -1 just as sine would be -1 and cosine would be 0 at 3/2 π. The full circle is completed at 2π where sine is again 1 and cosine is 0. When you see it graphically it looks like this:

Check out this video here keeping in mind that π is approximately 3.14 and 2π is around 6.28.

 

I found my review of the unitary circle really fun. Let me know if I have made any mistakes here by leaving a comment.

 

This just happened today

 

Words of Encouragement

 

 

On faulty premises, faulty results and faulty procedures

This is part 2 of my post on Trigonometry and measuring trees.

 

I made this post in two parts because a lot of learning has happened this week that would be overwhelming, both to write and to read, in only one post. I left off with the grand task of measuring my Christmas tree. I felt it would be very simple, since I could do the calculations and then measure the tree directly to check them. I had only one problem, I could not find a protractor at home.

 

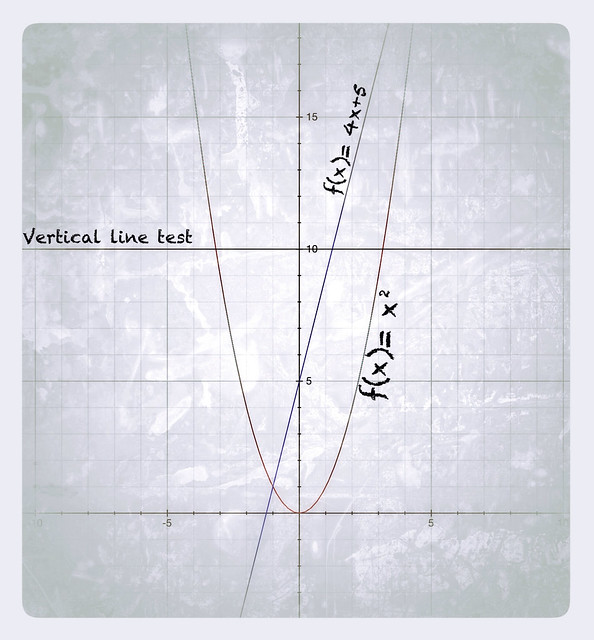
You see, the way we measured our school when I was in tenth grade was by standing an x distance from the wall and, using a protractor, we would measure the angle from our the spot we stood to the top of the school. That way we could use the tangent formula tanθ=opposite side/adjacent side, and get:

 

Tan(angle) x (distance from wall) = height of school

 

To make up for the lack of protractor I rummaged the App Store to find al alternative. I needed an app that would measure the angle of inclination of the phone as I used it to look at the top of the christmas tree. I settled on Angle Meter.

 

This app lets me lift the iPhone and measure the angle of inclination. It's purpose is to use the camera as a viewer and to measure the angles of what you are looking at.Their site will explain it better that I just have. The app was very sensitive and it took me a few tries to figure out how to tweak it for my purpose, like subtracting 90 deg from the angle shown.

 

When I felt ready I took the distance from my position to the tree. Then I measured the angle (making sure I subtracted 90 deg from the angle I got) by placing the iPhone on a small table to keep it steady. I plugged these two measurements into the equation above. And got the height of the tree as seen in the picture. Simple right?

Not so. Even as I went to be thrilled about what I had just done, a clearer mind next morning showed me my mistake. You see, I did not get a perfect result the first time. So I kept at it a few times thinking the problem was the sensitivity of the app measuring the angle. At the distance I was from the tree, a .10deg difference was almost a 12 inch difference.

In my first attempt, the record of which I sadly erased, my measurement came up short...by a lot. That was immensely frustrating. Then once I knew the hight of the tree, I kept measuring to get the right angle. I at least was honest with myself enough as to try to "get" that angle by using the phone app to measure the top of the tree. Therefore once I succeeded, it felt like a true accomplishment. What then did the morning reveal?

 

The next morning I realized that it was impossible for my calculations to be right since I did not account for the height of the table I had placed my phone on. If you look at the diagram of the figure measuring the school, you will notice that in order to get the true height of the school you will need to ad the height from the floor to the compass. The reason my first measurement was short, could have been because I needed to account for the table's height.

 

What is important to keep in mind is that I got a "right" result because I knew what that result should be and I did not stop until I got it. The phrase "even a broken watch is right twice a day" comes to mind.

 

The realization of my mistake was a blow. Even though my efforts at learning Calculus are only for self growth, the fact that I could have given incorrect data of that magnitude, without realizing it, was disturbing. I pledge from now on to double check all my work for follies like these.

 

To rectify my mistake, I regrouped and tried another approach. Even when the Angle Measure app was very good at what it did, I was using it for a different purpose. I decided to get a different app whose purpose was closer to what I needed. That is how I got to Easy Angle, an app that takes a picture and then let's you measure angles in it. I grabbed my tape measure and looked for something to measure.

I found a column in a parking structure and measured 120 inches from that column with my tape measure. I left the tape measure in place and stepped back to take the picture with the Easy Angle app. Using the tape measure as a guide aI measured the angle. I had to repeat that process a couple of times to get horizontal line exactly right. At least the Easy Angle app kept the photo static so I could work on it over and over. Once I got that horizontal line just right (35.31 deg), I ran the numbers. That column should be 85 inches. And according to my tape measure, that column is about 85" tall.

The bottom line of my adventure is that one should always be aware that knowing what a result should be can influence the process of getting that result.

It is like finding only what one wants or expects to find.I put forth a very situation that sometimes happens to people. A flat tire early in the morning.

When one gets a flat tire at the start of the day, it is normal to think : This is going to be a bad day. And sure enough, most of the time the day is quite horrible. Yet, was the day horrible because it was "destined" to be a bad day? Or did were we just looking for bad things to happened and made every little nuisance a bad thing?

That is the question in life and in math.

I appreciate your feedback so sound off in the comments and let me know how I am doing.

 

Posted with Blogsy

Words of Encouragment

 

 

On trigonometry and measuring trees pt.1

I love trigonometry. It is that weird kind of complicated love one has for a subject that its tough enough for you to be glad you left it behind, but cool enough to pursue from time to time.

 

I can still recite the Pythagorean theorem by heart: The square of the sum of the "legs" of a triangle equals the square of the hypotenuse.

Before my review I had a hazy recollection of sines, cosines and tangents. I remembered their graphs being waves and that they were interrelated somehow.

 

What I did remember was that in high school we measured the height of our school using trigonometry. On that assigment my calculations were off enough to get less than 90% of the points. I had not thought about that in years, but I know it bothered me back then, since I knew no one had gone and measured that wall directly...so how could I know the teacher was right? The fact that the teacher, Mr. Quintero, had been doing this for years, and that countless of students had done this calculation accurately before me did not enter my mind then. I just focused on trying to prove I could be right.

 

After all that history, let me surmise a little of what I have reviewed of trigonometry. Trigonometry is the study of triangles, specifically those with one right (90 deg) angle. The relationships of the sides of that triangle gives us the Pythagorean theorem.

 

From the relationships of the sides and angles of those right triangles we get the trig functions sine, cosine and tangent.

Therefore, following the rules in the picture, if we know any two sides, or any side and one angle other than the 90% one. We can solve all other angles and sides. At first glance this information sounds baffling, but trigonometry is one of those fields in mathematics that is immensely practical.

To know that as long as you can draw an accurate right triangle, the relationships of its sides remain the same so mater how big or small that triangle is, is simply amazing. In fact, it is one of those constants in nature, alongside Pi, that makes mathematics such a transcendental discipline. One that has spawn more than a few religions, as Pythagorans might attest to.

 

During my review I ran into at least 2 exercises of measuring trees. They would give me the distance to the tree and the angle of elevation to the top of the tree. With that I must be able to calculate the height. But how?

 

Well, if you look at the picture of the triangle above and compare it to the data. You can conclude that I have been given the value of the adjacent side (the lenght between me and the tree) and the angle θ (the elevation from my point of view to the top branch of the tree). What I need to find out then, is the lenght of the opposite side (height of the tree). Do any of the formulas above have the two given variables and the unknown variable?

 

Yes, tanθ. We know that tanθ = opposite/adjacent. If we need to find the height of the opposite side we rearrange the formula to opposite = tanθ(adjacent). Which means that the lenght of the opposite side equals the tangent of the degree corresponding to that side times the lenght of the adjacent side to that angle.

 

Let's imagine this example: We are standing 30 feet away from a tree. We lie flat on our stomach, take a protractor and use it to see the topmost branch of the tree. When we do so, the angle of inclination is given as 53.13 degrees. How tall is the tree?

We just derived that opposite = tanθ(adjacent), substituting our given data we get. Opposite=tan(53.13)(30 feet) or opposite=(1.33)(30 feet). That would make our tree approximately 39.9 feet tall. Cool, right?

Well, not content with the excercises alone I decided to do a real world measurement. However, considering my past experience measuring the height of my high school and not having any direct measurement for it, I decided to try it on a tree I could measure. So, I used our Christmas tree. I'll tell you all about it in my next post.

Feel free to add your comments bellow.

 

Just got enrolled in PreCalculus with Coursera

Well, I took a break from my trigonometry review went and took the plunge. I am enrolled now in a Pre-Calculus course with Coursera and the University of California, Irvine. I've been hearing about Coursera for a few months now but I never got the urge to take a look at what it was about.

 

 

 

I could try to explain what I believe Coursera to be, but I'll leave it to their About section. You can read it in full here.

About Coursera

We are a social entrepreneurship company that partners with the top universities in the world to offer courses online for anyone to take, for free. We envision a future where the top universities are educating not only thousands of students, but millions. Our technology enables the best professors to teach tens or hundreds of thousands of students.

Through this, we hope to give everyone access to the world-class education that has so far been available only to a select few. We want to empower people with education that will improve their lives, the lives of their families, and the communities they live in.

 

I am fairly excited about this. It will be a way to do my own studying but with a class like structure. The workload of 10 to 12 hours a week sounds a little daunting, we'll see how that plays out. What I like about it is that it will last 10 weeks. That seems reasonable. I am always second guessing myself about the speed in which I am going through my review.

 

I plan to take a Calculus course after that. Tha way I can answer one of the questions that have bothered me from the beginning of this journey which is...

How will I know if I had learned Calculus?

The final test for the Calculus course and my progress through it will say I do...or not. And your input will also be invaluable. Let me know what you think of this idea.

 

Words of Encouragment

 

On remembering why I love Math and Completing the Square

I just finished function theory and went straight to polynomials. It was refreshing to meet and work with these old friends of mine. And unlike a week ago, I was a little readier to meet this:
ax² + bx + c = 0
 

On January 5th, I wrote about my rude awakening when I realized I remember a lot less math, that I thought. The example I wrote about was a transformation of ax² + bx + c = 0 to

 
Well, guess what?, not only can I now do the transformation myself and understand its significance, but the journey to learning it made me remember why I loved math. I'll show you the process I penciled in.

I would be lying if I said this progress did not thrill me. I am experiencing the same excitement I used to get in high school when things started to click. In the grand scheme of things, the transformation I just did is trivial. However, within the process, I was reminded to do a step that, for me, it is the magic of mathematics. I got to ad a number to both sides of the equation that was not there before.
 
Yes, indeed. In ordert to go from ax² + bx + c = 0 to I had to use a technique called, completing the square. That technique allows us to remove the exponent of x² in order to have only x variables in the equation.
Therefore if I wanted to express ax² + bx + c = 0 in terms of x I would need to do the following.

First I need to get rid of the coefficient a in ax² that is done by the whole polynomial dividing by a:
x² + ^b/_ax + ^c/_a = 0.
 
Then we pass the non-variable term to the other side of the equation.
x² + ^b/_ax = - ^c/_a
 
Now here is where the magic happens. When we study quadratic formulas we learn that x² +2bx +b² is a perfect square that can be expressed as (x + b) ². So in theory whenever we get an equation that fits the mold x² + 2bx, we can ad +b² (which would mean half of whatever number b is and then squaring that number) on both sides of the equation and complete the square. I will do that to our main equation bellow.
 
 
x² + ^b/_ax + (^b/_2a)² = - ^c/_a + (^b/_2a)²


Now we can get


(x + ^b/_2a)² = (^b/_2a)² - ^c/_a

And after simplifying we get.

(x + ^b/_2a)² = ^b2/_4a² - ^c/_a


 
 
Then applying another technique I love, we take ^c/_a and transform it into something we can subtract from ^b2/_4a². All we need to do is multiply it by ^4a/_4a , the equivalent of multiplying by one, thus leaving the term unchanged.

Now we have

(x + ^b/_2a)² = ^b2/_4a² - ^4ac/_4a²
 
Which finally simplifies to
 
(x + ^b/_2a)² = ^{b2 - 4ac}/_4a²
 
 
And there it is. What caused me so much grief a week ago, now is understood. But more importantly, I rediscovered two powerful tools in mathematics.
 
1) All thigs being equal...we can add a term or operation to both side of an = sign and not change it.
So if x = c, the x +1 = c +1; and (x+1)² = (c+1)²
 
2) Identity
Math is a language. It describes our world. Therefore it should not be surprising that it does things we do in real life.
For example, number 1 is both 1 and 1/1, and 100/100, and 1² , and 4-3, etc. They are all 1. However, if I am dealing with money knowing that I can express 1 dollar as 100/100 cents is really useful.
 
The same things happens with people. If you have a brother, he is also your mother's (or father's) son, he is your grandmother's grandson, your uncle's nephew, etc. In some contexts it would be more important for someone to know your brother as your grandmother's grandson, than as your uncle's nephew.
 
Isn't math great? Let me know what you think in the comments.
 

This is getting real

I just bought a textbook (used) and notebook (new and awesome) to help my studies.
 
I hope my notebook gets found one day by guy like Charlie from the series numb3rs, and he says something like: "Most of the stuff here makes no sense, it has to be a coded message. I'll run a Yoda-Shatner probability test to crack it."

 

 

Words of encouragement

 

 

Quick update: On finishing functions and colorblindness

I am about to finish my review on basic functions. Since I finished the calcFTWfree chapter I wanted to check out other resources on function to make sure I did not miss anything. In iBooks store I found this, for a lack of a better word, book:
School Yourself Hands on Pre-Calculus
I hesitate to call it a book because it is so much more. For example, it has interactive exercises and even video explanations within the pages you are reading.
 
In the functions section you can play around with functions and even make your own by dragging your finger along an x,y plane. It's seriously cool and I would have loved to have something like that back in school. To make it even better, it's free. If you know any kid who is struggling through pre-calculus because he or she cannot wrap their heads around the concepts, let them know about this book. They will need access to an ipad or ipad mini.
 

Getting back on track, In the middle of one of the hands-on exercises on positive or negative functions (part of functions whose outputs are in the positive or negative side of the y axis), the exercise looks like the picture opposite.
 
Everything was great until I realized the chart was supposed to have two colors, one for the segment over the x axis and another for the segment under it.
 
The problem is I could only see one color, because I am colorblind.
 
Colorblindness is a condition that affects between 1% to 10% of males and less than .05% of women depending on what studies you look at. It is not vision loss, so it is usually labeled as a chromatic deficiency. For a medical explanation on colorblindness you can go here.

My colorblindness is usually, at most, a nuisance. I have learned to live with it. I know what color clothes to buy so they would match. I have taught myself to recognize colors by association and references. And most of the time I can live a very normal life with it. My condition does have its drawbacks. I need as second set of eyes when I am cooking, or eating, meat at any term bellow well done. I would also have trouble describing a car's color after a hit and run, as I experienced once. If you would like to know what it feels like to be colorblind from someone who can explain it better than I ever could, see this 9 minute documentary called There is no such thing as color. If you want the short and sweet version checkout the 3 1/2 minute video at the bottom of that page, it's made for kids but I found it very enlightening.
 

 

Getting back to my problem with the chart, I decided to write the people of SchoolYourself with a suggestion of making the color changes more distinct, or even better, to use a dashed line to differentiate both segments to help colorblind people "see" them better. To my amazement they answered the same day, thank me for the comment, and told me they will make recommendations for future editions. That was a great response time...did I mention their book is free? And just in case, I am in no way affiliated to SchoolYourself other than as a consumer of their book.

 

Let me know in a comment about other ways I can review my functions.

 

Update: The engineers in charge of SchoolYourself wrote me again with a picture that incorporated my suggestions into their charts to make them easier to see by people with Colorblindness. They asked for my feedback. I was sincerely touched by this effort. They now have a fan for life.

On one-on-one equations & discovering the attributes of self-learning

It has been an interesting week. From making a bold resolution enthusiastically, to learning how challenging the task will be, I can say I've had a great time. I think that the endeavor of learning calculus will end up giving me deeper insight into other fields of education. Mainly on self-learning.
 
As an example I will give you my lesson today on One-to-One equations using the CalcFTWFree app.
 
First let me tell you what I understood as a one-to-one function: it is the type of option that every number you input has only one number output that is not repeated again. So if you input numbers say from 1 to infinity into it, you would get an infinite stream of numbers that never repeat. So that, for example, if you input a 1 and you get a 2, there is no other input number that will give you a 2 again.
 
The notation used to demostrate this is if two functions (function of x1 and function of x2) are equal and x1 and x2 are equal, that function is one-to-one.
 
Here is what I told you, in algebraic form, from the CalcFTWfree app. The example worked is 4(x1)+5 = 4(x2)+5.
 

A function is called a one-to-one function if

f(x1)=f(x2)⇒x1=x2

We start with the left hand side and get to the right hand side:

f(x1)=f(x2)

⇒4(x1)+5=4(x2)+5

⇒4x1+5−5=4x2+5−5

⇒4x1=4x2

⇒4x1(1/4)=4x2(1/4)

⇒x1=x2

I was able to follow the proof of it very well. Then a thought entered my mind.
 

How can I prove a function is not one-to-one?

It hit me there and there that if I had a teacher, I could just ask her (or him). Since I did not, I had to use my resourcefulness to first try to figure it out on my own, or find the answer somewhere.
 
I know from the horizontal line test, that quadratic equations, those of the f(x)=x² variety, create "U" shaped graphs that fail the horizontal test.

But what I got was this:
 
(x1)² = (x2)²

√(x1)² = √(x2)²

^{x1 = x2}

And...I just got further confused. According to my calculations f(x)=x² is a one-to-one equation. I mean I followed the same steps as the proof above and got an answer I know it's wrong. But what went wrong? Had I had a teacher with me, I now know it would have saved me hours of finding out. On the other hand, scourging the Internet to get to the bottom of the problem helped me get different perspectives on how to solve this problem.
 
Thank got I found this in here, I paste or bellow with some modifications in illustration.
 

Example

: Define h: R R is defined by the rule h(n) = 2n². Prove that h is not one-to-one by giving a counter example.

Counter example:

Let n₁ = 3 and n₂ = -3. Then

2(n1)² = 2(n2)²

2(3)² = 2(-3)²

18 = 18

Hence h(n₁) = h(n₂) but n₁ n₂, and therefore h is not one-to-one.

Aha! Ok, so even when my previous calculations told me (x1)² = (x2)², I failed to realize that x1 and x2 could be different. You see, after some hours working on this I remembered my teachers telling me that quadratic equations have two solutions one is positive, and one is negative.

Therefore if you input a 3 in h(n) = 2n² you will get 18. If the only way to get the number 18 in that formula would be to put input a 3 the formula would be one-to-one, however if you put -3 in there you will also get 18.

A teacher would have told me that in a few minutes, that would have allowed me to go further. Without a teacher, I was forced to go deeper. Is one approach better than the other? I guess that would depend on the goal.

 

Words of encouragement and wisdom

 

I'll need more of these. If you've got any, send them my way

 

 

Of humbleness and understanding your domain

On New Year's Day, I felt really confident on my quest to learn Calculus. I would say over confident. Even after getting excellent advice on where to start (Pre Calculus), I pushed on with the Calculus books I had. Then I hit the wall. Yes, The Wall. The wall of realization that I was getting nowhere. The wall that has a sign that says:"if you are here and do not know what to do next, you missed a step, go back and return when ready."
Hitting that wall was (and still is) painful because of my pride.
 
Had I been humble, and realized I had not done math like this in a long time, I would have started from a math place I am still comfortable with. But no, I believed myself to be just a little fuzzy about quadratic equations and trigonometry. Oh, how wrong I was. How wrong was I? Would you like to know? Ok, let's give you an example of a phrase I found in the MIT Calculus for beginners page that baffled me.
 

The equation ax² + bx + c = 0 can be rewritten (when a is not 0, after dividing by a) as

That my friends is just an algebraic manipulation. A simple exercise in the grand scheme of things. Still, I could not follow the steps taken to get there. That was my wake up call. I need to go back to pre-calculus, back to functions, back to the last place I feel comfortable with.

That's how I landed in general function theory. I mean I work with functions all the time. How many calls have got in a weeks time? How much have we paid in cable over the last year? How much has our kilowatt hour fluctuated in 3 years? I love graphing things out, so I should start there, right?

Wrong.

Because when I tried starting with general function theory I ran into this gem in wikipedia when reviewing domains (which the course tells me is very important for pre-calculus and calculus problems)

For a function

defined by

, or equivalently ,

the codomain of f is , but f does not map to any negative number. Thus the image of f is the set ; i.e., the interval [0, ∞).

I must have stared at those statements for 5 minutes straight, before realizing that I had no idea what they meant. The English I got...but the symbols baffled me. After much rumination, and 6 hours of sleep, I went back to them and did what I should have done from the start. Went even further back to get the notations right.

Translation (as best I could come up with): , means for a function with a domain (the universe of numbers you will input into a function) of the Real Number (numbers that you can put on a graph) and a codomain (all the numbers the function could assumed as defined even when the function won't output all values in that codomain) that is also all Real numbers.

That translation took me an hour, and half a dozen websites to produce...but hey, that's progress.

Let me know if I am on the right track!

 

What I'm using to learn Calculus

OK, I will be going digital on this project. So I have the following:

 
1) iTunes U course:
 

Calculus I

MA005

Saylor Foundation, The Saylor Foundation

Created: 04/10/12 Updated: 10/04/12

Suggested duration: 15 weeks.

2) MIT's Calculus for Beginners and Artist

http://www-math.mit.edu/~djk/calculus_beginners/index.html

3) Quickgraph App: As a graphic calculator...it makes me miss my TI-85 a little less.

And 4 other apps that I will use as reference. I also plan to got to YouTube and Wikipedia. There, I just alienated any academic that stumbled through here.

There is another resource I will be using and that is hopefully you. I don't know who you are, or for that matter if there will ever be a you, but guess what, your input is important: mathematical and otherwise.

If you think there is anything else I should get let me know in the comments.

 

A little background for all this

Learning Calculus has been my goal for a very long time. When I arrived to the University of Puerto Rico in 1996, I held a medal for Mathematics, among other subjects, and an aced AP advanced math test that propelled me for classes ahead of other first-years. I was very excited to take my Pre-Calculus course. It was nerve-racking because I was selected to take a condensed section of Pre-Calculus, that was supposed to be two semesters, in one term.
 
Then, about a third into that semester, my life changed dramatically. My father, who was my math mentor when I thought no one could get me out of the woods of polynomials, died in a car accident. That left me and my younger brother parent-less. We had lost our mom 3 years earlier.
 
I read somewhere that Calculus is the study of change...well no calculations could have helped me cope with what I had gone through that day. I battled on for the rest of the semester but it was hard. I just couldn't concentrate on my classes. I got a C in that Pre-Calculus class. I was in such denial of what had happened in my family that I credited the grade to my lack of ability to understand calculus.
After that my life took me away from mathematics. Whenever I face problems that involved math beyond algebra, I shunned them. Still, a part of me knew I was just shortchanging myself.
 
So little by little, I have come back to the world of math. Actually my favorite tool for exploring it has been excel. Once you get me started with equations, its hard to quit them. Now after 17 years I made myself a promise. I would learn and master Calculus because I owe it to myself. I owe myself to know if I truly have a limitation in learning it, which will put me at par with most of the wonderful people I know, or if it was something that I can do after being ready to.
 
That is the question this journey will answer.
 
Please fell free to comment. I don't want to take this journey alone.
 
 

Back to Basics

Well, I got my answer from Quora as to where should I start to learn Calculus and, as I feared, it's clear, balanced and reasonable.

"I would retake Pre-Calculus first. Not because you got a, "C," in it in college but because Pre-Calculus is largely review of all the material you will need to know for Calculus.I would [not] try learning by yourself; you may lose motivation that way. Instead, sign up at a local community college and take classes there. The textbook is probably going to be your biggest expense." From Henry Maldonado @ Quora.

As much as I would like to think that my Math is where it was 17 years ago, I know there's a lot I have forgotten. So pre-calc it is...
 

Ok, so where should I start?

Let's try the collective wisdom of Quora:
 

 
I always feel self conscious when I use Quora, I usually get a swift lesson on English grammar and the correct way to ask a question. Still, it's the best place to go for crowd sourcing answers...now I wait.
 

Letter of intent?

Calculus was first discovered, if I may use that word instead of invented, either by a 23 year old Issac Newton or by a 28 year old Gottfried Leibniz, in 1666 or 1674 respectively. Now, approximately 34 decades since that discovery, a 34 year-old, husband, father and professional, is trying to learn it...for no practical reason, other than to reach a long-delayed personal goal