On one-on-one equations & discovering the attributes of self-learning

It has been an interesting week. From making a bold resolution enthusiastically, to learning how challenging the task will be, I can say I've had a great time. I think that the endeavor of learning calculus will end up giving me deeper insight into other fields of education. Mainly on self-learning.
 
As an example I will give you my lesson today on One-to-One equations using the CalcFTWFree app.
 
First let me tell you what I understood as a one-to-one function: it is the type of option that every number you input has only one number output that is not repeated again. So if you input numbers say from 1 to infinity into it, you would get an infinite stream of numbers that never repeat. So that, for example, if you input a 1 and you get a 2, there is no other input number that will give you a 2 again.
 
The notation used to demostrate this is if two functions (function of x1 and function of x2) are equal and x1 and x2 are equal, that function is one-to-one.
 
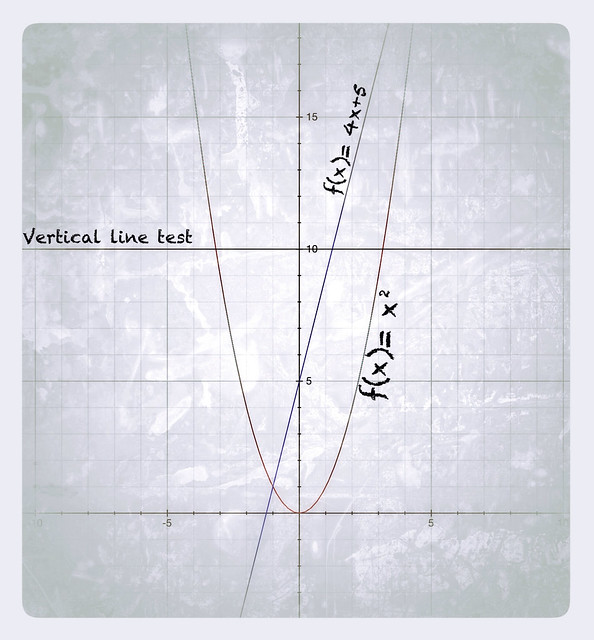
Here is what I told you, in algebraic form, from the CalcFTWfree app. The example worked is 4(x1)+5 = 4(x2)+5.
 

A function is called a one-to-one function if

f(x1)=f(x2)⇒x1=x2

We start with the left hand side and get to the right hand side:

f(x1)=f(x2)

⇒4(x1)+5=4(x2)+5

⇒4x1+5−5=4x2+5−5

⇒4x1=4x2

⇒4x1(1/4)=4x2(1/4)

⇒x1=x2

I was able to follow the proof of it very well. Then a thought entered my mind.
 

How can I prove a function is not one-to-one?

It hit me there and there that if I had a teacher, I could just ask her (or him). Since I did not, I had to use my resourcefulness to first try to figure it out on my own, or find the answer somewhere.
 
I know from the horizontal line test, that quadratic equations, those of the f(x)=x² variety, create "U" shaped graphs that fail the horizontal test.

But what I got was this:
 
(x1)² = (x2)²

√(x1)² = √(x2)²

^{x1 = x2}

And...I just got further confused. According to my calculations f(x)=x² is a one-to-one equation. I mean I followed the same steps as the proof above and got an answer I know it's wrong. But what went wrong? Had I had a teacher with me, I now know it would have saved me hours of finding out. On the other hand, scourging the Internet to get to the bottom of the problem helped me get different perspectives on how to solve this problem.
 
Thank got I found this in here, I paste or bellow with some modifications in illustration.
 

Example

: Define h: R R is defined by the rule h(n) = 2n². Prove that h is not one-to-one by giving a counter example.

Counter example:

Let n₁ = 3 and n₂ = -3. Then

2(n1)² = 2(n2)²

2(3)² = 2(-3)²

18 = 18

Hence h(n₁) = h(n₂) but n₁ n₂, and therefore h is not one-to-one.

Aha! Ok, so even when my previous calculations told me (x1)² = (x2)², I failed to realize that x1 and x2 could be different. You see, after some hours working on this I remembered my teachers telling me that quadratic equations have two solutions one is positive, and one is negative.

Therefore if you input a 3 in h(n) = 2n² you will get 18. If the only way to get the number 18 in that formula would be to put input a 3 the formula would be one-to-one, however if you put -3 in there you will also get 18.

A teacher would have told me that in a few minutes, that would have allowed me to go further. Without a teacher, I was forced to go deeper. Is one approach better than the other? I guess that would depend on the goal.