Limit existence and infinity

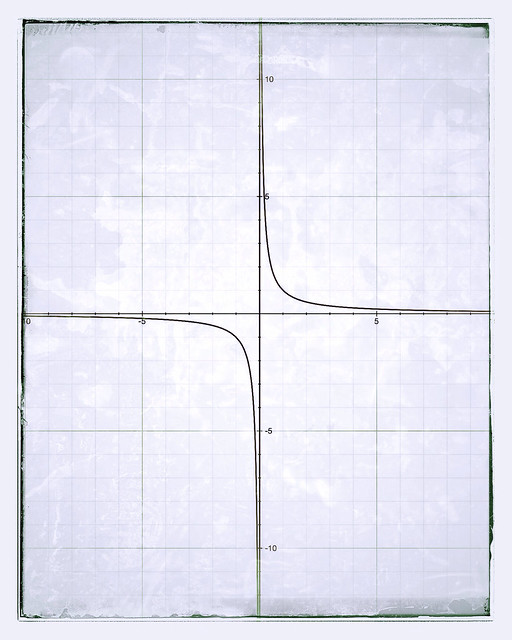
One if the awesome things about studying on my own, is the flexibility of choosing my own schedule and resources. The drawback, as I have mentioned before, is that different resources have different points, methods and even explanations. If your resources also vary in timeframe, those issues become more apparent. Let's take for example the limits of 1/x as x approaches 0 from the negative and from the positive side.

If we look at a graph of 1/x we can see that as x approaches 0 from the negative side, the graph starts to approach the y axis but not touch it. Since x cannot be 0 (1/0 is undefined), then the y axis, where x=0, is an asymptote, a line that will never be touched by the graph. That means that our graph will get closer and closer to the y axis for all infinity without touching it. Therefore the limit of 1/x as x approaches 0 from the negative side, in the strictest definition of a limit, does not exist and that is how my text book defines it.

My online class however, also defines this limit as negative infinity and as positive infinity when you approach 0 from the positive side. The Profesor explained that it was a more informative way to describe the limit of 1/x as x approaches 0.

My problem came along when I did my textbook homework after my online lesson. While I was checking my answers I noticed I had gotten two incorrect ones. They were the limits described above. In the textbook the right answer was that the limits did not exist, I had answered that they were positive and negative Infiniti. Being a student on my own, I had to retrace my steps, watched my class again and do a lot of research to find out if I had gotten the right answer. When I reviewed my online lesson I heard the explanation the professor made about these limits not existing and how using infinity gave us more info about what was happening.

If I had not been able to re-watch my class, I would probably still be looking for the answer. In a traditional classroom my doubt would have been put to rest in a second by the teacher. On my own I had to figure it out myself. I see advantages and disadvantages to both situations.

How about you?

 

On limits and life

These last two weeks I've been studying limits in various ways, from various sources, and different media. I've used videos, sites, ebooks, paper books, ad apps. It is great to see how each reference approaches the topic differently, and how the central concepts emerge from the gathering of information.

I am starting to see why many people regard Calculus as beautiful. Being able to find the equation of a line that is tangent to a curve using limits is breathtaking. I am not kidding. There was something awe inspiring when out of some algebra and some elementary Calculus I arrived at a formula, that when graphed, touched a curve at exactly one point before continuing in its path. Can you see the significance of that? These two functions for an instant, touched, and then moved on.

To delve deeper into this existential stream of consciousness about Calculus, consider that a limit tells us about where a function is heading. It doesn't care about what happens when the function gets there. It cares more about what happens as it gets closer and closer to a given point. Therefore, in Calculus as in life, the most important thing is the journey rather than the destination.That gets me to think about the people we meet briefly once in our lives. Those chance encounters might not change our paths, but there is a cosmic record that they happened. At that moment when two people meet briefly, you can describe each of them as being together. In other words we could say that at 9:00pm on Sunday, May 19th, 2013, John met Mary and Mary met John. Therefore John and Mary became part, in that instant, of the greater formula of life as variables sharing the same time and space coordinates. And that point in time, much like a limit, gives us information about where each of them is and how they are behaving.

I am liking this calculus stuff more and more each day.

Let me know your thoughts.