If you can draw a graph on a piece of paper without lifting your pencil once, that graph is continuous. In other words, there are no holes, jumps or asymptotes that block its process. My project of learning calculus is, by this definition, not continuous.
Continuity seems to be important enough in Calculus that every book I've seen has a section dedicated to it. However, it's heartening that, as I have learned, continuity is not crucial for determining limits. As long as the graph is approaching the same number from both sides there will be a limit even if there is a hole at that number. Therefore, I estipulate that as long as I am approaching my goal of learning calculus this year, I am allowed a couple of holes here and there.
When a graph is continuous, the limit of a function as x approaches a is f(a). In other words, if I know function x+1 is always continuous, then the limit of x+1 as x approaches 2 is f(2) which equals 3. The information that the graph is continuous let's me know that I can substitute the number I want to take a limit of into an equation without running the risk getting an undefined expression like dividing by zero.
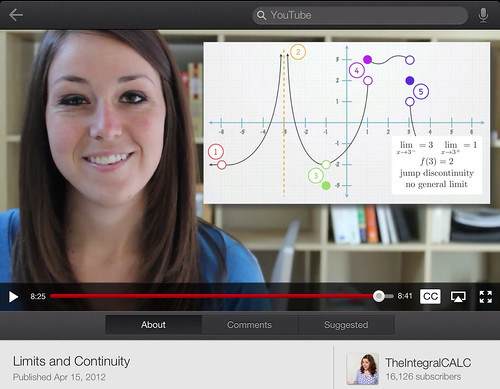
Most of the calculus I have been doing so far deals with discontinuities. And I imagine that in the end it is discontinuities that will be a major part of my studies.
For a good brief intro to basic calculus and discontinuities you can try this video. I found its series in YouTube and really like it since it reminds me of the format of my coursera Pre-Calculus videos.
I plan to minimize future discontinuities in my studies, if possible, and get back to a more productive rhythm. This calculus stuff is getting ever more fascinating and I want to get and see it all.
Let me know your thoughts.